目标：

• 我了解Harris Corner Detection背后的概念。
• 函数：cv.cornerHarris()，cv.cornerSubPix()

理论

在上一节我们已经知道了角点的一个特性：向任何方向移动变化都很大。Chris_Harris 和 Mike_Stephens 早在 1988 年的文章《A CombinedCorner and Edge Detector》中就已经提出了焦点检测的方法，被称为Harris 角点检测。他把这个简单的想法转换成了数学形式。将窗口向各个方向移动（u，v）然后计算所有差异的总和。表示如下：

$$E(u,v) = \sum_{x,y} \underbrace{w(x,y)}\text{window function} , [\underbrace{I(x+u,y+v)}\text{shifted intensity}-\underbrace{I(x,y)}_\text{intensity}]^2$$

窗口函数可以是正常的矩形窗口也可以是对每一个像素给予不同权重的高斯窗口。

角点检测中要使 E (µ,ν) 的值最大。这就是说必须使方程右侧的第二项的取值最大。对上面的等式进行泰勒级数展开然后再通过几步数学换算（可以参考其他标准教材），我们得到下面的等式：

$$E(u,v) \approx \begin{bmatrix} u & v \end{bmatrix} M \begin{bmatrix} u \ v \end{bmatrix}$$

其中：

$$M = \sum_{x,y} w(x,y) \begin{bmatrix}I_x I_x & I_x I_y \ I_x I_y & I_y I_y \end{bmatrix}$$

这里，$$I_x$$和$$I_y$$分别是x和y方向上的图像导数。（可以使用函数cv.Sobel()轻松找到）。

然后是主要部分。在此之后，他们创建了一个分数，基本上是一个等式，它将确定一个窗口是否可以包含一个角点。

$$R = det(M) - k(trace(M))^2$$

其中：

• $$R = det(M) - k(trace(M))^2$$
• $$trace(M) = \lambda_1 + \lambda_2$$
• $$\lambda_1$$和$$\lambda_2$$是M的本征值

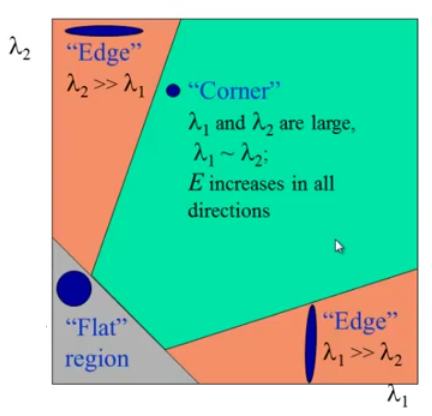
因此，这些特征值的值决定区域是角点，边缘还是平坦。

• 当$|R|$很小，当$\lambda_1$和$\lambda_2$很小时，该区域是平坦的。
• 当$R<0$时，在$\lambda_1 >> \lambda_2$时发生，反之亦然，该区域是边缘。
• 当R很大时，当$\lambda_1$和$\lambda_2$大并且$\lambda_1 \sim \lambda_2$时发生，该区域是拐角。

它可以用下面这张很好理解的图片表示：

因此Harris角点检测的结果是一个由角点分数构成的灰度图像。选取适当的阈值对结果图像进行二值化我们就检测到了图像中的角点。我们将用一个简单的图片来演示一下。

OpenCV中的Harris角点探测器

为此，OpenCV具有函数cv.cornerHarris()。它的参数是：

• img - 输入图像，应该是灰度和float32类型。
• blockSize - 考虑角点检测的邻域大小
• ksize - 使用的Sobel衍生物的孔径参数。
• k - 方程中的Harris检测器自由参数。

请参阅以下示例：

import numpy as np
import cv2 as cv

filename = 'chessboard.png'
img = cv.imread(filename)
gray = cv.cvtColor(img,cv.COLOR_BGR2GRAY)

gray = np.float32(gray)
dst = cv.cornerHarris(gray,2,3,0.04)

#result is dilated for marking the corners, not important
dst = cv.dilate(dst,None)

# Threshold for an optimal value, it may vary depending on the image.
img[dst>0.01*dst.max()]=[0,0,255]

cv.imshow('dst',img)
if cv.waitKey(0) & 0xff == 27:
    cv.destroyAllWindows()

以下是三个结果：

具有亚像素精度的角点

有时，你可能需要以最高精度找到角点。OpenCV附带了一个函数cv.cornerSubPix()，它进一步细化了以亚像素精度检测到的角点。以下是一个例子。像往常一样，我们需要先找到Harris的角点。然后我们传递这些角的质心（角点处可能有一堆像素，我们采用它们的质心）来细化它们。Harris角以红色像素标记，精致角以绿色像素标记。对于此函数，我们必须定义何时停止迭代的标准。我们在指定的迭代次数或达到一定精度后停止它，以先发生者为准。我们还需要定义它将搜索角点的邻域大小。

import numpy as np
import cv2 as cv

filename = 'chessboard2.jpg'
img = cv.imread(filename)
gray = cv.cvtColor(img,cv.COLOR_BGR2GRAY)

# find Harris corners
gray = np.float32(gray)
dst = cv.cornerHarris(gray,2,3,0.04)
dst = cv.dilate(dst,None)
ret, dst = cv.threshold(dst,0.01*dst.max(),255,0)
dst = np.uint8(dst)

# find centroids
ret, labels, stats, centroids = cv.connectedComponentsWithStats(dst)

# define the criteria to stop and refine the corners
criteria = (cv.TERM_CRITERIA_EPS + cv.TERM_CRITERIA_MAX_ITER, 100, 0.001)
corners = cv.cornerSubPix(gray,np.float32(centroids),(5,5),(-1,-1),criteria)

# Now draw them
res = np.hstack((centroids,corners))
res = np.int0(res)
img[res[:,1],res[:,0]]=[0,0,255]
img[res[:,3],res[:,2]] = [0,255,0]

cv.imwrite('subpixel5.png',img)

下面是结果，其中一些重要位置显示在缩放窗口中以显示：